Modal Analysis of a “Tongue Drum”
[EDIT]: Updated to a later version of MATLAB (2019a), so code has been updated to suit. Also, see the follow up for time domain simulations!
We’ve had a look at using finite element analysis to solve the wave equation in 2D geometries to find room modes and resonances (here), so the next step up is 3D geometries. Again, we’ll use MATLAB’s PDE toolbox to view the modal structure of a simple percussion instrument, something resembling a “Tongue” or “Hang” drum.
Creating the Geometry
For 3D models, MATLAB requires .stl files, which can be created using a number of popular 3D modelling software packages. For this project, I learned a bit of Blender, which I eventually got doing what I wanted, but I had a lot of trouble with MATLAB not liking certain geometries. Potentially, other programs would be more suited to the task for creating and exporting relatively simple geometries such as these (maybe SketchUp?).
For reference, the drum geometry is (roughly) an inverted bowl 20cm in diameter, 10cm high and 3mm thick, with two tongues of different sizes in the top surface.

Setting up the Model
The general procedure for setting up the MATLAB model is:
- Import the geometry
- Keep an eye out for import errors, it took a while to be able to create a geometrically valid .stl model.
- Mesh the geometry
- Play around with the mesh size parameters if needed.
- Define the material parameters
- In this case, we use the values for (approximately) steel.
- Set up the model coefficients
- Refer to this MATLAB example for further details
Running the Model
Running the model is pretty simple (especially with the newer version of the PDE toolbox). The results object contains the natural frequencies and the mode shapes.
Visualising the Results
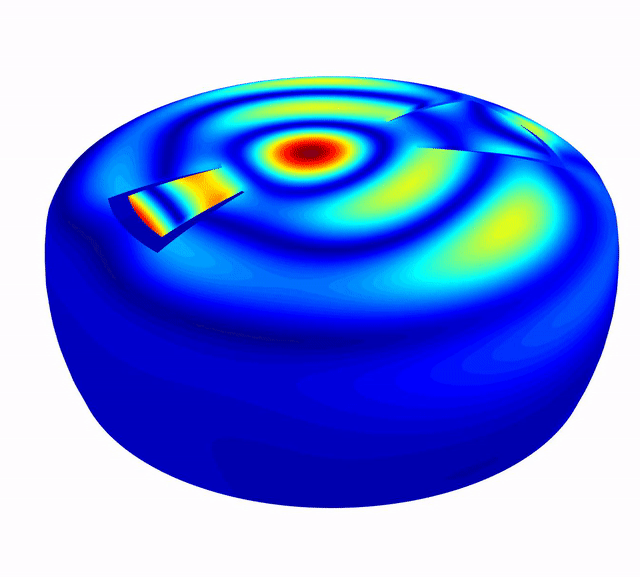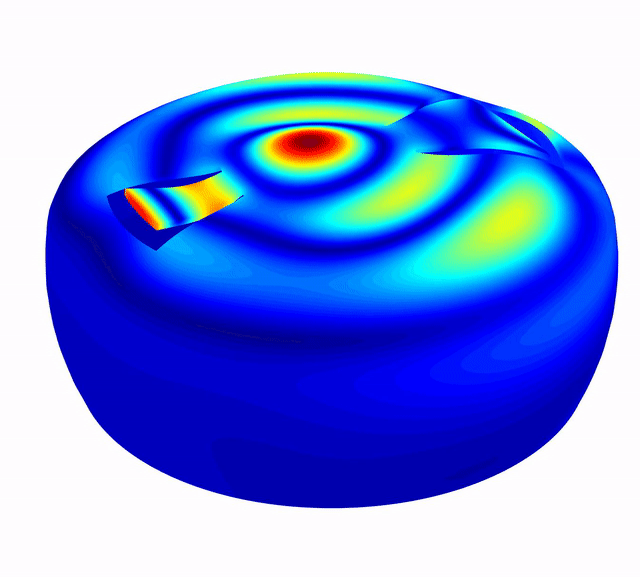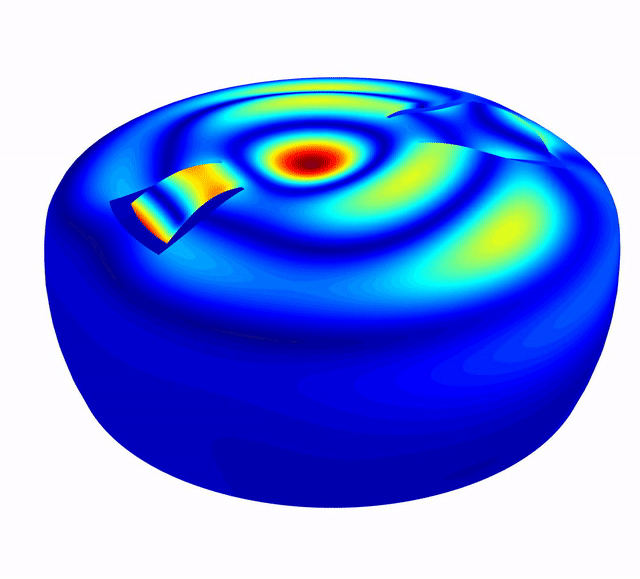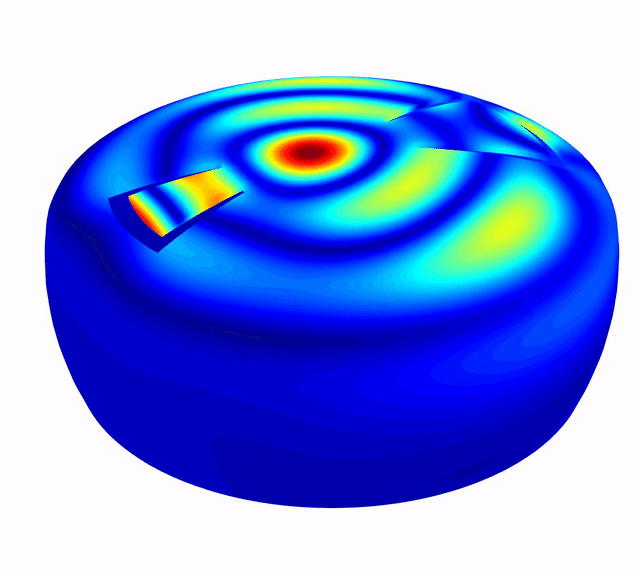
There are a number of ways to view the results, but perhaps the easiest and most accessible (and beautiful) is via animation. So here is an animated selection of modes of the tongue drum!
Some basic details
- The colour map shows blue areas as those that do not deviate much from their static position (nodes), going up to red, which are areas of maximum deflection (antinodes).
- The deflection has been scaled arbitrarily to be visually noticeable and pleasing. Actual deflections would be much less!
- For useful comparison, every animation is on the same time scale, which means the lower frequency modes don’t appear to “wiggle” that much, but I promise you that they do.
Discussion
Beautiful right?
In the first video, we clearly see what I call the “bell” modes, the standing waves around the open rim of the bowl. These are quite clearly related to the bowl diameter, and continue up into the higher frequencies in the same pattern.
The second video shows the first couple of “note” modes, the vibration of the tuned tongues of the drum. The first two of these are clearly a “flappy” mode as the fundamental of the note, and then a “twisty” mode present as an overtone. These are quite isolated on the tongues only.
As we increase in frequency, things start getting more interesting, as the modes of the tongues become similar to the modes of the top rounded surface – we start to see more interactions between the tongues and other drum surfaces.
Interestingly, there is very little, if any excitation/interaction between the bell modes and modes on the top plate, which I expect is due to my poor instrument design. The bowl is quite sharply bent, and this extra structural stiffness (which can be thought of as a impedance gradient in the material) serves to keep the vibrations in the top plate isolated from vibrations around the rim. A better designed drum might have a smoother shape to allow the whole drum to resonate, and have a more interesting acoustic presence.
Code
As always, here is the code. Run under MATLAB 2019a (finally upgraded!)
%% Geometry
% Initialise a 3D PDE model, and import the geometry
model = createpde('structural','modal-solid');
importGeometry(model, 'tongue_drum.stl');
% Visualise the Geometry
figure(1)
hc = pdegplot(model, 'FaceLabels', 'on');
hc(1).FaceAlpha = 0.6;
%% Properties
% Approximates steel
E = 180e9; % Modulus of elasticity in Pascals
nu = .265; % Poisson's ratio
rho = 8000; % Material density in kg/m^3
%% Set up the PDE coefficients
% Refer to https://au.mathworks.com/help/pde/examples/structural-dynamics-of-tuning-fork.html
% for further details
structuralProperties(model,'YoungsModulus',E,...
'PoissonsRatio', nu,...
'MassDensity', rho);
%% Mesh the Geometry
hmax = 0.0025;
generateMesh(model,'Hmax',hmax,'GeometricOrder','quadratic');
% Visualise the mesh
figure(1)
pdeplot3D(model);
title('Meshed Geometry');
%% Solve the model
freqRange = 2*pi*[100,5000] % [Hz] Only search for modes within these frequencies
results = solve(model,'FrequencyRange', freqRange);
%% Animate and Save Mode Vibrations
scaleFactor = 0.0005; % scale the vibrations for a better visualisation
modeSelection = 1:size(results.NaturalFrequencies,1); % animate and plot
animateMode(model,results, scaleFactor, modeSelection);
function frames = animateMode(model, result, scale, modes)
% Number of animation frames
nFrames = 360;
% Retrieve the base geometry data (undeformed)
[nodes,elements,T] = meshToPet(model.Mesh);
% Calculate the simulation timings.
% Find the associated mode frequencies
omega = result.NaturalFrequencies;
% Use a time period that covers one period of the lowest frequency mode of
% interest.
timePeriod = 2*pi./omega(min(modes));
% Cover the time period in the required number of frames.
t = linspace(0,timePeriod,nFrames);
% Set up the figure
h = figure('units','normalized','outerposition',[0 0 1 1]);
% Handle each mode seperately
for m = 1:length(modes)
modeID = modes(m);
for n = 1:nFrames
% The eigenvector represents the deformation from the static
% solution for a particular eigenvalue
% Construct the modal deformation and its displacement magnitude.
modalDeformation = [result.ModeShapes.ux(:,modeID), ...
result.ModeShapes.uy(:,modeID), ...
result.ModeShapes.uz(:,modeID)]';
modalDeformationMag = sqrt(sum(modalDeformation(:,:).^2,1));
% Compute the location of the deformed mesh at the current
% timestep
nodesDeformed = nodes + ...
scale.*modalDeformation*sin(omega(modeID).*t(n));
% Plot the deformed mesh with magnitude of mesh as color plot.
pdeplot3D(nodesDeformed,T,'ColorMapData', modalDeformationMag)
% Add an annotation. The usual title(...) method gets crazy with
% the rotating axes in 3D, so its easiest to use a uicontrol text
% label which remains static. Looks a bit ugly though.
uicontrol(h,'Style','Text','String',sprintf(['Mode %d, ', ...
'Frequency = %g Hz\n',...
'time (ms) = %.4f'], ...
modeID,...
omega(modeID)/(2*pi),...
t(n)*1000.0 ),...
'Units','Normalized','Position', [.4, .8,.2,.05],'FontSize',18)
% Clean up the plots a bit
colorbar off
delete(findall(gca,'type','quiver'));
qt = findall(gca,'type','text');
set(qt(1:3),'Visible','off')
axis equal
% Set the camera and lighting
camproj perspective
camva(25)
lighting gouraud
[cx, cy,cz] = camPath(t(n), timePeriod);
campos([cx, cy, cz])
camtarget([0,0,0])
% Finally, retrieve and store the frame
frames(n) = getframe(h);
end
% Save the video
saveVid(frames,sprintf('mode_%d.avi',modeID))
end
end
function [x, y, z] = camPath(t,timePeriod)
% Defines a camera path which circles the object once in a timePeriod,
% while oscillating above and below the object.
rotation = 2*pi;
x = .6*cos(rotation*t/timePeriod);
y = .6*sin(rotation*t/timePeriod);
z= 0.3*cos(2*pi*t/timePeriod)+0.1;
end
function saveVid( frames, title )
% Helper function which saves the video stored in frames.
v = VideoWriter(title);
open(v)
for frameNum = 1:length(frames)
writeVideo(v,frames(frameNum))
end
close(v)
end